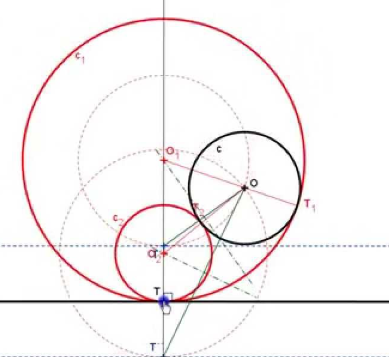
La dilatación es una transformación geométrica que permite resolver problemas de tangencias al modificar proporcionalmente las dimensiones de las figuras, manteniendo sus propiedades esenciales. Este método es especialmente útil en los problemas de Apolonio, donde se busca una circunferencia que sea tangente a tres elementos dados, que pueden ser puntos, rectas o circunferencias.
Aplicación de la Dilatación en Problemas de Apolonio
En el siguiente video se presentan tres ejercicios que ilustran cómo aplicar la dilatación para resolver diferentes casos de tangencias:
- Circunferencia tangente a dos circunferencias y pasando por un punto dado (CCP)
- Circunferencia tangente a una circunferencia, una recta y pasando por un punto dado (CRP)
- Circunferencia tangente a dos rectas y pasando por un punto dado (RRP)
- Circunferencia tangente a dos circunferencias y pasando por un punto dado (CCP):
- Elementos dados: Dos circunferencias y un punto exterior.
- Objetivo: Encontrar una circunferencia que sea tangente a las dos circunferencias dadas y que pase por el punto especificado.
- Procedimiento:
- Identificación de elementos homotéticos: Determinar las circunferencias y el punto que se relacionan mediante una homotecia.
- Aplicación de la dilatación: Modificar proporcionalmente las dimensiones de las circunferencias para simplificar el problema.
- Resolución del problema simplificado: Una vez dilatadas las figuras, resolver el problema de tangencia en la nueva configuración.
- Reversión de la dilatación: Aplicar la transformación inversa para obtener la solución en la configuración original.
- Circunferencia tangente a una circunferencia, una recta y pasando por un punto dado (CRP):
- Elementos dados: Una circunferencia, una recta y un punto exterior.
- Objetivo: Encontrar una circunferencia que sea tangente a la circunferencia y a la recta dadas, y que pase por el punto especificado.
- Procedimiento:
- Identificación de elementos homotéticos: Determinar la relación de homotecia entre la circunferencia y la recta.
- Aplicación de la dilatación: Ajustar las dimensiones de las figuras para facilitar la resolución del problema.
- Resolución del problema simplificado: Resolver la tangencia en la configuración dilatada.
- Reversión de la dilatación: Aplicar la transformación inversa para obtener la solución en la configuración original.
- Circunferencia tangente a dos rectas y pasando por un punto dado (RRP):
- Elementos dados: Dos rectas y un punto exterior.
- Objetivo: Encontrar una circunferencia que sea tangente a las dos rectas dadas y que pase por el punto especificado.
- Procedimiento:
- Identificación de elementos homotéticos: Determinar la relación de homotecia entre las dos rectas.
- Aplicación de la dilatación: Modificar las dimensiones de las rectas para simplificar el problema.
- Resolución del problema simplificado: Resolver la tangencia en la nueva configuración.
- Reversión de la dilatación: Aplicar la transformación inversa para obtener la solución en la configuración original.
Conclusión
El método de dilatación es una herramienta útil para resolver problemas de tangencias complejos, especialmente en los casos planteados por Apolonio. Al aplicar una transformación que modifica proporcionalmente las dimensiones de las figuras, se simplifica la configuración geométrica, facilitando la identificación de soluciones. Es fundamental comprender las relaciones de homotecia entre los elementos dados y aplicar correctamente las transformaciones para obtener soluciones precisas.
Para una comprensión más profunda y visual de estos procedimientos, se recomienda visualizar el siguiente video completo:
Descarga la forma de resolver todos los problemas en el siguiente archivo: