POTENCIA - VECINDAE

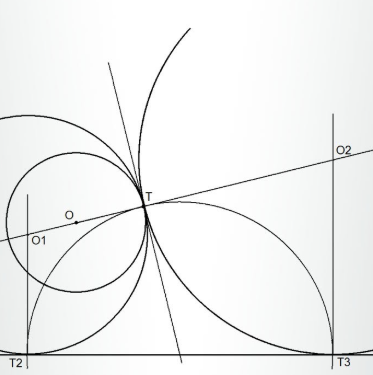
El método de potencia en tangencias geométricas

El método de potencia es una herramienta clave para resolver problemas de tangencia geométrica cuando solo contamos con un haz de centros o cuando necesitamos trabajar con relaciones de distancia entre circunferencias. Este método se basa en el concepto de potencia de un punto respecto a una circunferencia, lo que nos permite determinar posiciones clave como el eje radical y el centro radical, fundamentales para resolver ciertos casos de tangencias.

Conceptos fundamentales

1. Potencia de un punto respecto a una circunferencia

La potencia de un punto respecto a una circunferencia es una medida que relaciona la posición de ese punto con la circunferencia. Se define como:

Si trazamos una línea desde el punto que corta a la circunferencia en dos puntos (AAA y BBB), la potencia es el producto de las distancias desde el punto a esos dos puntos de intersección.

En otras palabras:

Si el punto está fuera de la circunferencia, la potencia es positiva.
Si el punto está sobre la circunferencia, la potencia es cero.
Si el punto está dentro de la circunferencia, la potencia es negativa.

Es una forma de medir cómo un punto “influye” en la circunferencia, y se utiliza para resolver problemas de tangencias y ejes radicales.

2. Eje radical

El eje radical entre dos circunferencias es el lugar geométrico de los puntos que tienen la misma potencia respecto a ambas circunferencias. Este eje es una recta perpendicular a la línea que une los centros de las circunferencias, y su posición depende de las relaciones entre los radios y la distancia entre los centros.

3. Centro radical

El centro radical es el punto donde se intersectan los ejes radicales de tres circunferencias. Este punto tiene la misma potencia respecto a las tres circunferencias.

1. Conceptos básicos del método de potencia

1.1. Potencia de un punto respecto a una circunferencia

La potencia de un punto PP respecto a una circunferencia es una medida geométrica definida como el producto de las distancias desde el punto PP a los dos puntos de intersección (AA y BB) de una recta trazada desde PP que corta la circunferencia.

1.2. Aplicación en tangencias

La potencia nos ayuda a localizar:

Puntos de tangencia (TT): Los puntos donde una circunferencia solución toca otros elementos.
Ejes radicales (ErEr): Rectas que representan lugares geométricos con la misma potencia respecto a dos circunferencias.
Centro radical (CrCr): Punto donde se intersectan los ejes radicales, útil para localizar soluciones.

2. Elementos clave del método

2.1. Haz de centros (HC)

Lugar geométrico donde se encuentran los centros de las circunferencias solución.
Se obtiene a partir de:
- Dos puntos: Mediatriz del segmento que los une.
- Dos rectas: Bisectriz del ángulo entre ambas.
- Punto y recta: Perpendicular desde el punto a la recta.
- Circunferencia y punto: Línea que une el centro de la circunferencia con el punto.

2.2. Circunferencia auxiliar (CA)

Herramienta gráfica adicional con radio arbitrario.
Debe cumplir:
- Pasar por los puntos del enunciado.
- No cruzar las circunferencias dadas (si son tangentes externas).

2.3. Ejes radicales (Er)

Lugar geométrico donde los puntos tienen igual potencia respecto a dos circunferencias.
Se obtiene:
- Como perpendicular al segmento que une los centros de las circunferencias.
- Usando una circunferencia auxiliar para trazar tangentes desde puntos conocidos.

2.4. Centro radical (Cr)

Punto donde se cortan los ejes radicales de dos o más circunferencias.
Es el lugar donde equidistan los puntos de tangencia con las circunferencias del problema.

3. Procedimiento general

Paso 1: Identificar el haz de centros (HC0)

Analiza los datos del problema (puntos, rectas o circunferencias).
Determina la línea o lugar geométrico donde se encontrarán los centros de la circunferencia solución.

Paso 2: Trazar la circunferencia auxiliar (CA)

Dibuja una circunferencia arbitraria que pase por los puntos dados o esté dentro de las circunferencias enunciadas.
Utiliza esta circunferencia para determinar ejes radicales o puntos auxiliares.

Paso 3: Calcular los ejes radicales (Er)

Usa las relaciones de potencia entre los elementos para encontrar las rectas de igual potencia respecto a las circunferencias dadas.
Si no hay suficiente información, se trazan más circunferencias auxiliares.

Paso 4: Localizar el centro radical (Cr)

Encuentra el punto de intersección de los ejes radicales. Este será el centro de la circunferencia solución.

Paso 5: Hallar los puntos de tangencia

Traza las rectas tangentes desde el centro radical hacia las circunferencias auxiliares o los elementos del enunciado.
Usa las propiedades de perpendicularidad para localizar los puntos de tangencia (TT).

Paso 6: Determinar los centros solución (HC1 y HC2)

Identifica los posibles centros solución (O1O_1 y O2O_2) sobre el haz de centros para definir las circunferencias solución.

4. Ejemplo práctico

Enunciado:

Hallar una circunferencia que sea tangente a dos circunferencias dadas (C1C_1 y C2C_2) y pase por un punto dado PP.

Resolución:

Determinar el haz de centros (HC0):
- Traza la línea que une los centros de las dos circunferencias.
- El haz de centros será perpendicular a esta línea.
Trazar la circunferencia auxiliar (CA):
- Dibuja una circunferencia con centro arbitrario en el haz de centros que pase por el punto PP.
Calcular los ejes radicales (Er):
- Encuentra las rectas de igual potencia entre la circunferencia auxiliar y las circunferencias dadas.
Localizar el centro radical (Cr):
- Identifica el punto de intersección de los ejes radicales.
Trazar la circunferencia solución:
- Con CrCr como centro, ajusta el radio para que la circunferencia pase por el punto PP y sea tangente a C1C_1 y C2C_2.

5. Casos comunes de tangencias resueltos por potencia

Circunferencia tangente a dos circunferencias exteriores.
Circunferencia tangente a dos circunferencias interiores.
Circunferencia tangente a una circunferencia interior y otra exterior.
Circunferencia tangente a una recta y una circunferencia.
Circunferencia tangente a dos rectas y una circunferencia.

Ejemplo práctico: Juego de canicas

Introducción

En dibujo técnico, resolver problemas de tangencias implica utilizar herramientas gráficas para hallar elementos como rectas, circunferencias y puntos que cumplan condiciones específicas de tangencia. En el caso del juego de las canicas, el objetivo es trazar una recta tangente que pase desde un punto dado y toque dos circunferencias (los aros) sin atravesarlas. Este problema se aborda utilizando conceptos básicos como el eje radical, los puntos de tangencia y las construcciones auxiliares.

Elementos fundamentales desde el dibujo técnico

1. El eje radical

El eje radical es una recta clave que se define gráficamente como el lugar geométrico donde un punto tiene la misma influencia (o potencia) respecto a dos circunferencias. Desde el dibujo técnico, esto se visualiza así:

Interpretación gráfica: Imagina dos circunferencias y traza la línea que une sus centros. El eje radical será una recta perpendicular a esta línea.
Significado práctico: Todos los puntos sobre esta recta tienen la misma distancia relativa a ambas circunferencias, lo que permite trazar soluciones tangentes de forma equilibrada.

2. Puntos de tangencia

Los puntos de tangencia son los puntos específicos donde la recta (trayectoria de la canica) roza las circunferencias. Desde el dibujo técnico, los puntos de tangencia tienen dos propiedades esenciales:

Están alineados con el centro de la circunferencia en una dirección perpendicular al radio.
Son los únicos puntos en los que la recta tangente no corta la circunferencia.

Resolución del problema con herramientas de dibujo técnico

Paso 1: Trazar los elementos dados

Dibuja las circunferencias:
- Ubica los centros de las dos circunferencias en el plano.
- Traza sus radios según el tamaño dado.
Marca el punto de lanzamiento:
- Ubica el punto desde el que lanzarás la canica.

Paso 2: Determinar el eje radical

Traza la línea que une los centros de las circunferencias:
- Con una regla, dibuja una línea recta entre los centros de las dos circunferencias.
Construye el eje radical:
- Con un cartabón, traza una recta perpendicular a la línea que une los centros. Ubica el eje radical en la posición correcta utilizando herramientas de medición para que divida de manera proporcional el espacio entre las circunferencias.

Paso 3: Localizar los puntos de tangencia

Trazar líneas auxiliares:
- Desde el punto de lanzamiento, traza líneas imaginarias hacia las circunferencias.
Identificar las tangencias:
- Ajusta las líneas hasta que se conviertan en tangentes a las circunferencias. Esto se verifica gráficamente al observar que la línea toca la circunferencia en un solo punto y forma un ángulo recto con el radio en ese punto.

Paso 4: Trazar la recta tangente

Conecta el punto de lanzamiento con los puntos de tangencia:
- Usa una regla para unir el punto de lanzamiento con cada punto de tangencia identificado. Estas líneas representan las trayectorias posibles para lanzar la canica.

Casos y vídeos

Los problemas de tangencia que se resuelven mediante el método de potencia tienen en común la necesidad de encontrar lugares geométricos clave como el eje radical, el centro radical, y los puntos de tangencia. Estos elementos permiten calcular la posición y el tamaño de la circunferencia solución en función de las condiciones iniciales. A continuación, describimos los casos más comunes, que incluyen combinaciones de recta (R), circunferencia (C) y punto (P). Los casos que abordaremos son:

PPR: Punto, punto, recta.
PRR: Punto, recta, recta.
RRC: Recta, recta, circunferencia.
CCP: Dos circunferencias y un punto en una de ellas.
CPP: Una circunferencia y dos puntos.
RCP (punto en la circunferencia): Una recta, una circunferencia y un punto sobre la circunferencia.
RCP (punto en la recta): Una recta, una circunferencia y un punto sobre la recta.

1. Caso PPR (Punto, Punto, Recta)

Elementos dados:

Dos puntos (P1P_1 y P2P_2).
Una recta (RR).

Descripción detallada:

Hallar una circunferencia que pase por los dos puntos y sea tangente a la recta.

Forma de resolución:

Traza la mediatriz del segmento que une P1P_1 y P2P_2 para obtener el haz de centros.
Traza una perpendicular desde el punto de tangencia en la recta hacia la mediatriz.
Localiza el centro de la circunferencia solución en la intersección de ambas líneas.
Ajusta el radio para que la circunferencia cumpla con las condiciones de tangencia.

Propiedades aplicadas:

La mediatriz garantiza la equidistancia del centro a los puntos dados.
La perpendicular asegura la tangencia con la recta.

2. Caso PRR (Punto, Recta, Recta)

Elementos dados:

Un punto (PP).
Dos rectas (R1R_1 y R2R_2).

Descripción detallada:

Hallar una circunferencia que pase por el punto y sea tangente a ambas rectas.

Forma de resolución:

Traza las bisectrices de los ángulos formados por las dos rectas. Estas representan los posibles haces de centros.
Localiza la posición del punto PP respecto a las bisectrices.
Ajusta el radio de la circunferencia para que toque ambas rectas y pase por el punto dado.

Propiedades aplicadas:

La bisectriz asegura la equidistancia del centro a ambas rectas.
El punto PP define la ubicación exacta de la circunferencia.

3. Caso RRC (Recta, Recta, Circunferencia)

Elementos dados:

Dos rectas (R1R_1 y R2R_2).
Una circunferencia (CC).

Descripción detallada:

Hallar una circunferencia que sea tangente a ambas rectas y a la circunferencia.

Forma de resolución:

Traza las bisectrices de los ángulos formados por las rectas.
Usa el eje radical entre la circunferencia y una circunferencia auxiliar para ajustar la solución.
Encuentra el centro radical en la intersección del eje radical con el haz de centros definido por las bisectrices.
Ajusta el radio para que la circunferencia sea tangente a los tres elementos.

Propiedades aplicadas:

Las bisectrices definen la posición del haz de centros.
El eje radical asegura que las potencias respecto a las circunferencias sean iguales.

4. Caso CCP (Dos circunferencias y un punto en una de ellas)

Elementos dados:

Dos circunferencias (C1C_1 y C2C_2).
Un punto (PP) situado sobre una de las circunferencias (C1C_1).

Descripción detallada:

Hallar una circunferencia que sea tangente a ambas circunferencias y pase por el punto dado.

Forma de resolución:

Traza la línea que une el centro de C1C_1 con el punto PP para obtener el haz de centros inicial.
Traza una circunferencia auxiliar que pase por PP y cumpla con las condiciones de tangencia.
Determina los ejes radicales entre la circunferencia auxiliar y C1C_1, y entre la circunferencia auxiliar y C2C_2.
Encuentra el centro radical en la intersección de los dos ejes radicales.
Ajusta el radio de la circunferencia solución para cumplir con la tangencia.

Propiedades aplicadas:

La tangencia se asegura ajustando el radio.
Los ejes radicales equilibran las potencias respecto a las dos circunferencias.

5. Caso CPP (Circunferencia y dos puntos)

Elementos dados:

Una circunferencia (CC).
Dos puntos (P1P_1 y P2P_2).

Descripción detallada:

Hallar una circunferencia que pase por los dos puntos y sea tangente a la circunferencia.

Forma de resolución:

Traza la mediatriz del segmento que une P1P_1 y P2P_2 para obtener el haz de centros.
Traza una circunferencia auxiliar que pase por P1P_1 y P2P_2.
Determina el eje radical entre la circunferencia auxiliar y CC.
Encuentra el centro radical en la intersección del eje radical con el haz de centros.
Ajusta el radio de la circunferencia solución para cumplir las condiciones de tangencia.

Propiedades aplicadas:

La mediatriz garantiza que el centro equidista de los puntos dados.
El eje radical ajusta la relación de potencia.

6. Caso RCP (punto en la circunferencia)

Elementos dados:

Una recta (RR).
Una circunferencia (CC).
Un punto (PP) situado sobre la circunferencia.

Descripción detallada:

Hallar una circunferencia que sea tangente a la recta y pase por el punto PP, siendo tangente a la circunferencia CC.

Forma de resolución:

Traza la línea que une el centro de CC con PP.
Usa esta línea como haz de centros inicial.
Traza una circunferencia auxiliar que cumpla las condiciones del problema (pasando por PP).
Encuentra el eje radical entre CC y la circunferencia auxiliar.
Localiza el centro radical en la intersección del eje radical con el haz de centros.

Propiedades aplicadas:

La tangencia implica que el radio sea perpendicular a la recta en el punto de contacto.
El eje radical asegura igual potencia respecto a las circunferencias.

7. Caso RCP (punto en la recta)

Elementos dados:

Una recta (RR).
Una circunferencia (CC).
Un punto (PP) situado sobre la recta.

Descripción detallada:

Hallar una circunferencia que sea tangente a la recta, pase por el punto PP, y sea tangente a la circunferencia CC.

Forma de resolución:

Traza una perpendicular desde el punto PP a la recta RR.
Usa esta línea como haz de centros.
Traza una circunferencia auxiliar que pase por PP.
Determina el eje radical entre la circunferencia auxiliar y CC.
Encuentra el centro radical en la intersección del eje radical con el haz de centros.